Hilbert Uzayı

Hilbert uzayı, Öklid uzayını nicem mekaniğiyle uyumlu biçime dönüştüren soyut vektör uzayı'dır. Pozitif skaler çarpımasahiptir. Matematik, fizik ve mühendislikte sıkça kullanılmaktadır. Adını David Hilbert'ten almaktadır. Hilbert uzayı matematiksel bir kavramdır,Öklid uzayı kavramının genelleştirilmesidir. iki-boyutlu Öklid düzlem ve üç boyutlu uzaydan Bu boyutların herhangi bir sonlu veya sonsuz sayıda uzayları için vektör cebri yöntemlerini uzatır. Bir Hilbert uzayı ölçülebilir uzunluk ve açı sağlayan bir iç çarpım yapısına sahip soyut bir vektör alanıdır. Ayrıca uzayın içinde yeterli sınırları varlığını öngören bir özelliğin kullanılabilir tekniklerine izin vermek için Hilbert uzayı tam olmalıdır.Hilbert uzayları genellikle sonsuz boyutlu fonksiyon uzayları gibi,matematik,fizik,ve mühendislikte doğal olarak ve sık sık ortaya çıkar. Erken Hilbert uzayları David Hilbert,Erhard Schmidtve Frigyes Riesz tarafından 20. yüzyılın ilk on yılında bu bakış açısından incelenmiştir.Bunlar kısmi diferansiyel denklemler,kuantum mekaniği,Fourier analizi (uygulamalar ve ısı transferi sinyal işleme içeren) ve termodinamik'in matematiksel temeli oluşturan ergodik teori'si,teorileri içinde vazgeçilmez araçlardır.John von Neumann,bu çok farklı uygulamaların altında yatan soyut bir kavram için Hilbert uzayı terimi icat etmiştir.Hilbert uzayı yöntemlerinin başarısı fonksiyonel analiz için çok verimli bir dönem başlatmıştır . bunun yanı sıra klasik Öklid alanlarından,integrallenebilir-karefonksiyonların uzaylarının içerdiği Hilbert uzayı,dizi uzayıları genelleştirilmiş fonksiyonların Sobolev uzayı'ndan ve holomorfik fonksiyonlar'ın Hardy uzayı'ndan oluşan örnekler. Geometrik sezgi Hilbert uzayı teorisinde birçok açıdan önemli bir rol oynar.bir Hilbert uzayıyla örtüşen Pisagor teoremi ve paralelkenar kurallarının tüm analogları.Daha derin bir düzeyde bir alt uzay üzerinde dik projeksiyon ( Bir üçgenin "irtifa bırakarak " analogu ) de optimizasyon problemleri ve teorinin diğer yönleri içinde önemli bir rol oynar. Bir Hilbert uzayının bir elemanı benzersiz düzlemde kartezyen koordinat ile benzer şekilde koordinat eksenleri (bir ortonormal taban),bir dizi ile ilgili kendi koordinatları belirtilebilir . Hilbert uzayı da yararlı toplanabilir-kare olan sonsuz diziler açısından düşünülebilir ki bu eksen sayılabilir sonsuz bir dizi,anlamına gelir. Bir Hilbert uzayında lineer operatörleri aynı şekilde oldukça somut nesnelerdir:tam anlamıyla karşılıklı dik yönlerde farklı faktörler tarafından alan germe dönüşümleri vardır.

Alıştırma örnekleri: Öklid uzayı

bir Hilbert uzayının en iyi ailevi örneğinden biri üç-boyutlu vektör'lerden oluşan Öklid uzayı'dır,R³ ile ifadesi,ve nokta çarpım ile donanımıdır,nokta çarpımda iki vektör alınır x ve y, ve bir gerçel sayı üretilir x·y. eğer x ve y Kartezyen koordinatlar içinde gösterilir, ise nokta çarpım

nokta çarpım tarafından tanımlanan özellikleri tatmin edicidir:

1. Bu x ve y içinde simetriktir: x · y = y · x.
2. Bu ilk değişken içinde doğrusal'dır : (ax₁ + bx₂) · y = ax₁ · y + bx₂ · y için herhangi skaler a, b, ve vektörler x₁, x₂, ve y.
3. It is pozitif tanım: bütün vektörler için x, x · x ≥ 0, ie eşitlikancak ve ancak x = 0.

vektörlerin çifti bir işlemci olarak,nokta-çarpım gibi,burada uygun üç özellik (gerçel) iç-çarpım olarak bilinir. Bir vektör uzayı donanımı ile bu tür bir iççarpım bir (gerçel)iç çarpım uzayı olarak bilinir. Her sonlu-boyutlu iç-çarpım uzayı yine bir Hilbert uzayıdır.Öklid geometrisi ile bağlantılı nokta çarpımın temel özelliği bu uzunluk her ikisi ile ilişkili olduğu bir vektörün (veya norm)'u,||x|| ile ifade edilir,ve iki vektör arası x ve y θ açısına formül yardımıyla

Çok değişkenli hesabı Öklid uzayı sınırları'nı hesaplayabilme yeteneğine dayanır ve bu sınırlar sonuç için yararlı kriterlere sahip. Birmatematiksel serisi

R³ içinde vektörlerin oluşumu mutlak yakınsak'tır, yakınsar uzunlukların sağlanan toplamı olarak bir gerçel sayıların düzgün serisi:^[1]

Sadece skalerlerin bir serisi olarak, mutlak olarak yakınsar vektörlerinin bir serisi anlamında,Öklid uzayında da bazı sınır vektör L 'ye yakınsar.

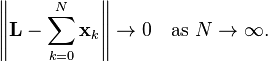
Bu özellik Öklid uzayı tamlığını ifade etmektedir: mutlak yakınsak bir dizi yalın anlamıyla yakınsar.

Tanım

Bir Hilbert uzayı H bir gerçel veya karmaşık iççarpım uzayı'dır buda bir tam metrik uzayı ile sırasıyla uzunluk fonksiyonu iççarpım tarafından uyarılır.^[2] Denebilirki Hkarmaşık bir iç çarpım uzayı anlamına gelir.Hbir iç çarpımın var olduğu bir kompleks vektör uzayıdır. elemanlarının her bir çifti için bir karmaşık sayı ilişkilendirerek H ın Bu, aşağıdaki özellikleri karşılayan x,y :

• Ögelerin bir çiftinin iç-çarpımı takas elemanlarının bir iç-çarpımının karmaşık eşleniğine eşittir :

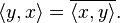
• İççarpımın doğrusal ilk bileşenin içindedir .^[3] a ve b bütün kompleks sayıları için,

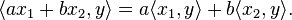
• Kendisi ile bir elemanın iç çarpımın pozitif tanımı'dır:

eşitlik durumunun tam tuttuğu(örtüştüğü) yer x = 0 sırasındadır.

Aşağıdaki şu iki özellik ikincil bileşen içindeki karşıt-doğrusal 1 ve 2'nin bir karmaşık iççarpımıdır,anlamı şudur

Gerçek bir iç çarpım uzay aynı şekilde tanımlanır,H dışında gerçek bir vektör uzayı ve iç çarpım gerçek değerleri alır.Böyle bir iç bir çarpımı doğrusal olacak:her bileşen içinde doğrusaldır. Bu norm gerçel-değerli fonksiyondur

ve uzunluk d ve x,y iki nokta arasında in H içinde tarafından norm açısından tanımlanmıştır

Burada bir uzunluk fonksiyonunun anlamı (1) şuki x ve yiçinde simetriktir, (2)x ve kendisi arası uzunluk sıfırdır,ve bunun dışında x ve y arası uzunluğu pozitif olmalıdır, ve (3) şuki üçgen eşitsizliği'ne uyar, anlamı şudur: xyz Diğer iki bacak uzunluklarının toplamından fazla olamaz:

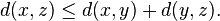
300px

Bu son özellik sonuçta daha temel Cauchy-Schwarz eşitsizliği'nin bir eşdizisidir, öyleki

eşitlik ancak ve ancak x ve y doğrusal bağımlılık iledir.

Bu şekilde tanımlanan bir mesafe fonksiyonuna göre, herhangi bir iç çarpım uzayı bir metrik uzay'dır, ve bazenön-Hilbert uzayı olarak bilinir.^[4] Herhangi pre-Hilbert uzayı Buna ek olarak aynı zamanda bir tam bir uzay Hilbert uzayıdır. Cauchy kriterlerinin Bütünlüğü bir formumuz üzerinden H dizisi içinde ifade edilir.: bir pre-Hilbert uzayı H tamdır.Eğer her Cauchy dizisi uzay içindeki bir ögeye Bu norm ile ilgili yakınsak ise, Bütünlük aşağıdaki eşdeğer durumu ile karakterize edilebilir: Eğer vektörlerin serisi 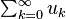 mutlak yakınsak anlamı

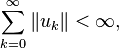
ise Hiçinde yakınsak seri , Kısmi toplamlar H unsuru yakınsama anlamındadır.

Tam normlu uzayı olarak, Hilbert uzayı tanımı gereği de Banach uzayı'dır. Böylece bunlar topolojik vektor uzayıdır, ki topolojik gösterim altkümenin açıklık ve kapalılıkgibi iyi-tanımlanmıştır.Bir Hilbert uzayının bir kapalı doğrusal alt-uzay'ının özel bir önemini taşımaktadır.Bu, kısıtlama ile oluşturulan iç çarpım,aynı zamanda tam(tam bir metrik uzayda kapalı bir küme olarak)ve bu nedenle kendi içinde bir Hilbert uzayıdır.

İkiincil örnek: dizi uzayı

bütün sonsuz dizi dizi uzayı ℓ² oluşturur,bu tür karmaşık sayılar serisi'nin z = (z₁,z₂,...)

yakınsak. İççarpım olarak ℓ² ile tanımlanıyor

Cauchy–Schwarz eşitsizliğinin bir eşdizisi olarak yakınsak ikinci serisi ile .

Uzay tamlığı sağlanan durum o zaman ℓ² 'nin öğeleri bir dizi mutlak yakınsak (norm içinde), ise ℓ²'nin bir ögeye yakınsamasıdır . Kanıtı matematiksel analiz içinde temeldir, ve Uzay elemanlarının matematiksel serisi sağlar karmaşık sayılar serisi ile aynı kolaylıkla işletilen olmaktadır(sonlu-boyutlu Öklid uzayında veya vektörleri)

kaynak: tr.wikipedia.org