Logaritma Hakkında Bilgi, Özelliklerive Kullanım Alanları

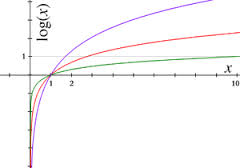
Logaritma, üstel işlevlerin tersinin hesaplanmasına duyulan ihtiyaç sonucunda ortaya çıkan matematiksel bir işlevdir. Logaritma, büyük değerleri daha kontrol edilebilir şekilde ifade etmeye yardımcı olan üsler olarak da tanımlanabilir.

Logaritma işlemi için “taban” adı verilen bir sayı seçilir, her sayının bu tabana göre logaritması alınır.

ax = A eşitliğinden logaritma alınarak

x = alog A eşitliği bulunur. Bu eşitlik “A’ nın a tabanına göre logaritması x’dir” diye okunur.

Logaritma Sistemleri

Kullanılmakta olan iki çeşit logaritma sistemi vardır. Bunlardan biri “Napier Logaritması”, öteki de “Ondalık Logaritma” (Bayağı Logaritma)dır. Birincisinde taban, a = 2,718281 diye alınır; ikincisinde a = 10 diye alınır. Napier logaritma sistemini 1614’te John Napier; ondalık logaritmayı ise daha sonra Napier ile birlikte Henry Briggs düzenlemiştir.

Logaritma, büyük çarpmaları, bölmeleri, basit toplamalara, çıkarmalara indirgemek için kullanılan bir yoldur, genel olarak, bir cetvel halinde gösterilir. Logaritma sayıları cebirde üs olarak yazılır.

Büyük sayıları çarpabilmek için matematikçiler bu sayıların sadece logaritmalarını toplarlar. Sonra logaritma cetvelinde, elde ettikleri yeni logaritmanın karşısındaki sayıyı bulur, böylece çarpmanın sonucunu elde ederler. Büyük sayılarla bölme işlemi yapılacaksa bu sefer bölen sayının logaritması, bölünecek sayının logaritmasından çıkarılır. Elde edilen sonuç, yeni bir logaritmadır. Bu logaritmanın, cetvelde, karşısındaki sayıya bakılınca, bölmenin sonucu bulunmuş olur.

Logaritmalardan, bölme, çarpma gibi işlemlerden başka, bir sayının karesini, kübünü, ya da kesirli üslerini (25,5 gibi) bulmakta da faydalanılır. Bir sayının karesi bulunmak isteniyorsa, o sayının logaritması 2 ile; kübü bulunmak isteniyorsa 3 ile çarpılır. Logaritmaların, ayrıca, büyük bir sayının köklerini bulmakta da sağladığı kolaylıklar vardır. Meselâ 271 sayısının küp kökü bulunmak isteniyorsa, önce logaritma cetvelinde bu sayının logaritması bulunur. Cetvele göre 271’in logaritması 2,4330’dur. Bu logaritmayı, küp kökü bulmak istediğimize göre, 3’e böleriz. Elde edilen sayı 0,8110’dur. Sonra bu sayının, logaritma cetvelinde, hangi sayının logaritması olduğu aranır. 0,8110 cetvele göre, 6,471’in logaritmasıdır. Demek ki 271’in küp kökü 6,471 ‘dir.

Logaritma Tarihçesi

Logaritma 17. yüzyılda birbirinden habersiz olarak çalışan John Napier ve Joost Bürgi tarafından keşfedilmiştir. Keşfedilmesinin ardından logaritma üzerine çalışan çok sayıda bilim insanından biri de 1700lü yıllarda yaşamış Türk bilim insanı Gelenbevi İsmail Efendi’dir.

Napier, Yunancada oran, orantı ve kelime anlamlarına gelen ‘logos’ ile sayı, rakam anlamına gelen ‘arithmos’ kelimelerinin bir araya getirerek işleve ‘logaritma’ ismini vermiştir.

Uzun zaman alan çok basamaklı çarpma işlemlerini kolaylaştırmak amacıyla oluşturulan logaritma, kısa sürece denizciler, bilim insanları ve mühendisler tarafından benimsenmiştir. Bu dönemde logaritma, hesap cetvelleri ve logaritma tabloları aracılığıyla kullanılmıştır.

18. yüzyılda Leonhard Euler, logaritmanın üstel işlevlerle olan ilişkisini farkına varmış ve bugünkü yazım biçimini oluşturmuştur.

Bugün çok sayıda hesap makinesi yalnızca 10 tabanında (log (x)), genel logaritmaları ve e tabanında (ln (x)), doğal logaritmaları hesaplamaktadır. ‘e’, 2.71828 sayısına eşittir ve pi sayısı gibi irrasyonel bir sayıdır. Bu sayı önce Napier’in Sabiti olarak anılmıştır. Sonraki dönemde ise, bugün de kullanıldığı şekliyle, Euler’in Sayısı olarak isimlendirilmiştir.

İkili Logaritma (2 Tabanında)

lb(x), ld (x), log (x), lg (x) veya log2 (x) olarak gösterilebilir. Bilgisayar bilimlerinde, bilgi kuramında, matematikte ve müzik kuramında kullanılır.

Doğal Logaritma (e Tabanında)

ln (x) veya log (x) olarak gösterilir. Matematiksel incelemelerde, fizikte, kimyada, istatistikte ve ekonomide kullanılır.

Adi Logaritma (10 Tabanında)

Genellikle lg (x) veya log (x) olarak; mühendislik, biyoloji ve astronomi alanlarında ise log10 (x) olarak gösterilir. Çeşitli mühendislik branşlarında, hesap makinesinde ve spektroskopide kullanılır.

Negatif Logaritma

Euler Özdeşliği kullanılarak negatif sayıların logaritması alınabilir.

İmajiner Logaritma 

Sanal logaritma olarak da adlandırılır. Sanal sayıları içerir. Negatif logaritmada olduğu gibi Euler Özdeşliğinden faydalanılır.

Logaritmanın Kullanım Alanları

Logaritma hem geometrik hem de aritmetik dizilerle ilişkili olduğu için gitar perdelerinin aralığı, mineral sertliği, yıldızlar, fırtına ve depremler gibi doğadan sanata kadar pek çok alanda kullanılır. Ayrıca logaritma, insanların içgüdüsel olarak sayıları ne şekilde düşündüklerini de açıklar.

Mekanik ve ardından elektronik hesap makinelerinin bulunmasından önce logaritma astronomiden yön bulmaya, ölçmeden mühendisliğe kadar çok sayıda alanda büyük bir önem taşıyordu. Örneğin; bir kağıtta 64 katman oluşturmak için kağıdı kaç defa katlamak gerekir sorusunu ele alalım. Kağıdı her seferinde ikiye katlamak gerekecektir. Logaritma kullanıldığında ise tabanı iki almak yeterli olacaktır. Bu da log2(64) = x olarak gösterilmektedir.

Logaritma artan çarpan değişiklikleri ile ilgili olduğundan, logaritmik ölçekler bilimsel ve gündelik olaylarda şaşırtıcı derecede fazla kullanılmakta ve hayatı kolaylaştırmaktadır. Logaritma, bulunuşunun üzerinden geçen yüzlerce yıl sonrasında hala ileri düzey matematik çalışmalarının merkezinde bulunmaktadır. 

Logaritmanın kullanıldığı alanlar genel olarak şu şekilde listelenebilir; 

• Notaların frekansları logaritmik bir sistemde dizilmiştir. Klasik Türk Müziğinde farklı makamlar arasındaki nota değişimi, farklı logaritmik tabanlar kullanılarak notalar için farklı frekanslar elde etme yöntemi ile sağlanabilir.
• Ses şiddeti birimi olan Desibel logaritmiktir.
• Depremin şiddetini hesaplayan Richter ölçeği logaritmayı kullanır.
• pH değeri logaritmik bir ifadedir ve pH ile pOH hesaplamaları logaritmiktir.
• Herhangi bir kaynağın gücünü Watt cinsinden ölçülmekte,
• Bilgisayarın yapımında, işletim sisteminin dizaynında ve bir algoritmanın hızını ölçmekte,
• Spektroskopide uyarılmış atom/normal atom oranında,
• Redoks tepkimelerinde,
• Kimya alanında kimyasal tepkimelerde hız konusunun ilerlemiş boyutlarında denge sabiti bulunurken,
• Denizcilik alanında matematiksel konumu verilen iki nokta arasındaki gerçek mesafeyi bulmakta,
• Nüfus artış tahminleri gibi istatistiksel değerlendirmelerde, bankacılıkta, bileşik faiz hesaplamalarında, fizyokimyada ve optikte de logaritma kullanılır.