Kaprekar Kimdir?
Shri Dattathreya Ramachandra Kaprekar 1905 ile 1986 yılları arasında yaşamış; sayılar teorisine katkılarda bulunmuş Hintli matematikçidir.
1905 yılında Hindistan’da Dahanu’da dünyaya geldi. Küçük yaşlardan itibaren sayılara duyduğu ilgi onu matematikçi olmaya yönlendirdi. 1929 yılında Bombay Üniversitesi’nden mezun oldu. 1930 yılından emekli olduğu 1960 yılına kadar Hindistan’da Devlali şehrinde matematik öğretmenliği yaptı.
Kendi adı ile anılan Kaprekar sayıları, Kaprekar sabiti, Kolumbiya sayıları, Harşad sayıları gibi kavramları matematik literatürüne katmıştır.
Kaprekar Sayıları
n basamaklı bir t kaprekar sayısının karesi alınıp sağdaki n basamağı solda kalan n-1 basamağına eklendiğinde sonuç yine t sayısını verir.
Örnek olarak:
55 sayısı iki basamaklı bir sayıdır.Önce karesi alınıyor.
552 = 3025 ,sonucunda sağdan iki basamak 25,soldan iki basamak 30 dur.
Burada 25 ile 30 u toplarsak ;30+25=55 sonuç sayının kendisini verir.
O zaman bu sayı bir kaprekar sayısıdır diyebiliriz.
1, 9, 45, 55, 99, 297, 703, 999, 2223, 4879 vb... sayılar da birer kaprekar sayılarıdır.
Kaprekar Sabiti
Hint matematikçi Kaprekar (1905-1986) tarafından tanımlanan, dört basamaklı sayılara en fazla yedi kez aşağıdaki işlemler uygulandığında ortaya çıkan sabit 6174 sayısı.
İşlemler, tüm basamakları aynı sayıdan oluşmayan (2222 gibi - ilk adımda sıfır sonucunu verecektir) ve herhangi üç basamağındaki sayılar aynı olup kalan bir basamaktaki sayı bu sayıdan bir büyük ya da bir küçük olmayan (1112, 5565 veya 8788 gibi - ilk adımda 999 sayısını verecektir) dört basamaklı sayılara uygulandığında en fazla yedi adımda sıfır veya6174 sabit sayısını verir.
- Yukarıdaki şartlara uygun dört basamaklı bir sayı alınır.
- Sayının basamaklarını büyükten küçüğe ve küçükten büyüğe doğru sıralayarak iki adet dört basamaklı sayı elde edilir.
- Elden edilen sayılardan büyükten küçüğü çıkarılır.
- 2. adım tekrar edilir.
En fazla yedi adımda sıfır ya da 6174 sabit sayısı elde edilecek ve kısır döngüye girilecektir.
Örnek:
  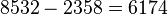 
|